今回は合成速度と相対速度について学びましょう。
どちらもベクトルとしてとらえることがとても大切です。ベクトルは、向きと大きさを持っている物理量なので、矢印で描くことがとても重要です。
合成速度と相対速度は結果の矢印の描き方が異なります。そこをきちんと理解しましょう。
また、合成速度の作図の仕方は、力の合成と同じ手順だということを覚えておいてください。
合成速度
合成速度の定義
合成速度とは、複数の速度を合成した速度を指します。
例えば、人が川で泳ぐ場合は、人の速度と川の速度の二つの影響を考える必要があるということです。
まずは、一直線上の速度の合成について考えましょう。
一直線上の速度の合成
一直線上の速度の合成は非常にシンプルです!(^O^)
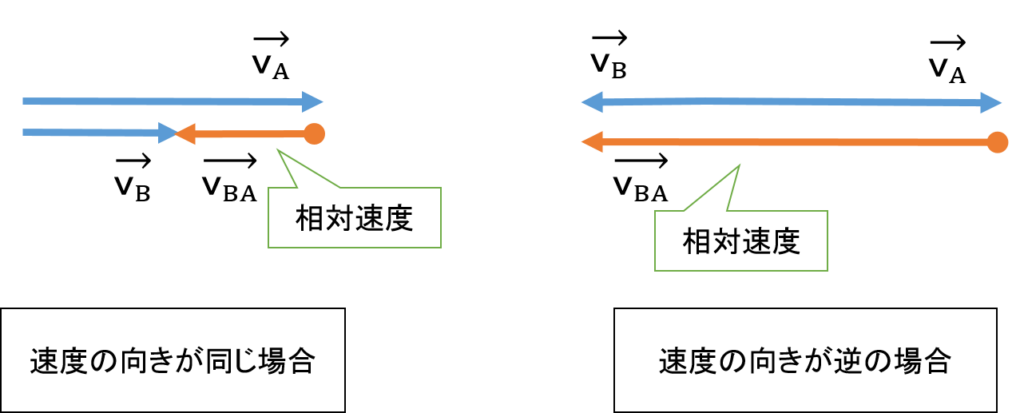
- 速度の向きが同じ向きの場合、矢印の長さをそのまま足します。
- 速度の向きが逆向きの場合、矢印の長さを打ち消し合います。
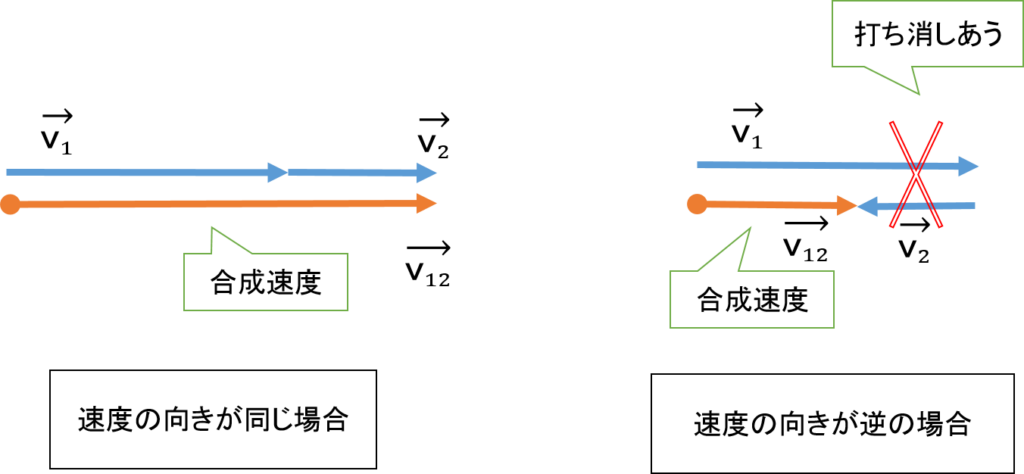
矢印をどんどん繋げて、最初の位置と最後の位置をつなげば合成速度の矢印ができます。
平面上の速度の合成
平面での合成速度を求める際には、問題文に出てきている数値をそのまま計算してはいけません!
必ず合成速度の矢印を作図し、作図した矢印(ベクトル)の大きさを求めましょう。
(平行四辺形を作るように作図しても可能です)

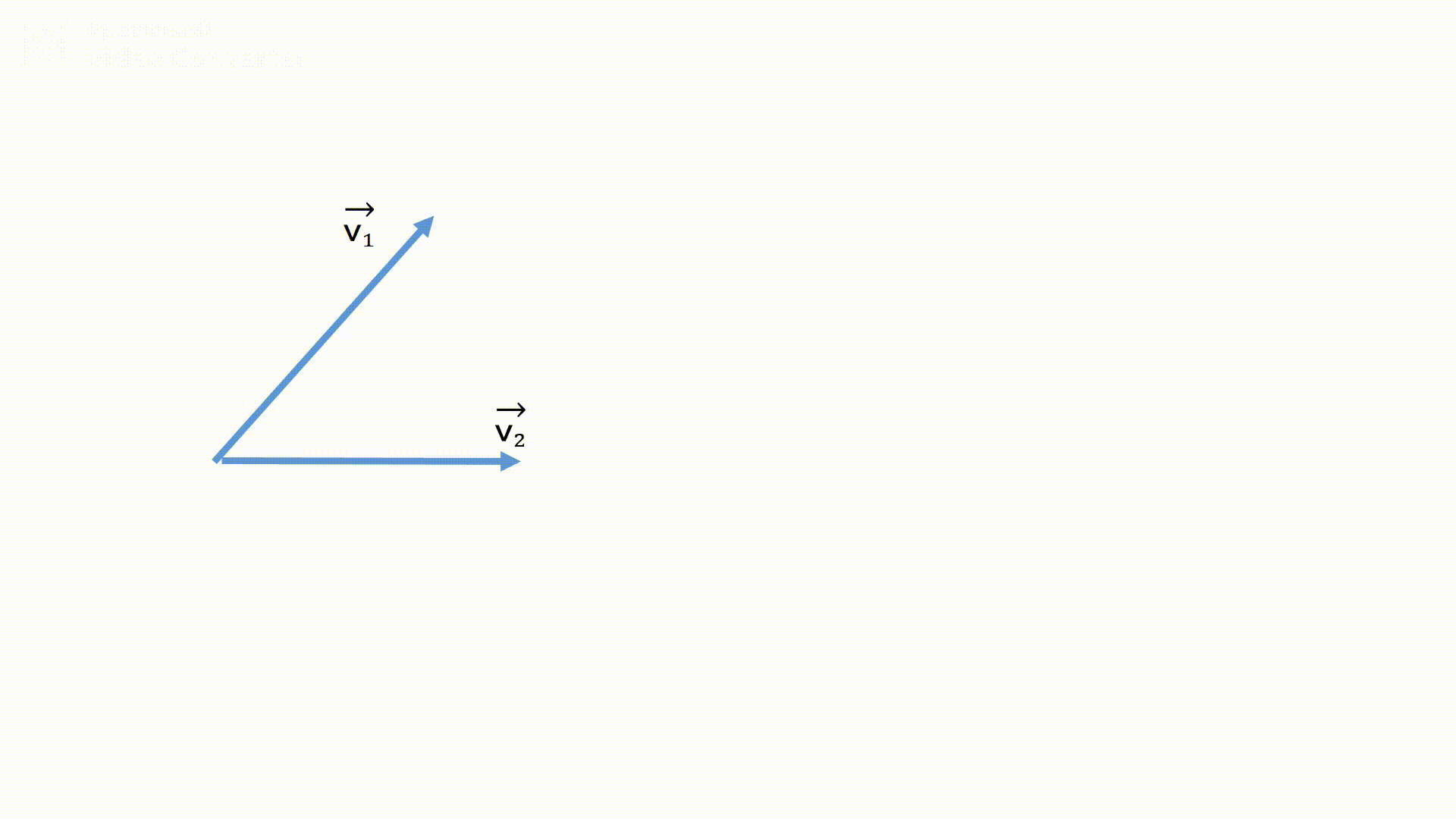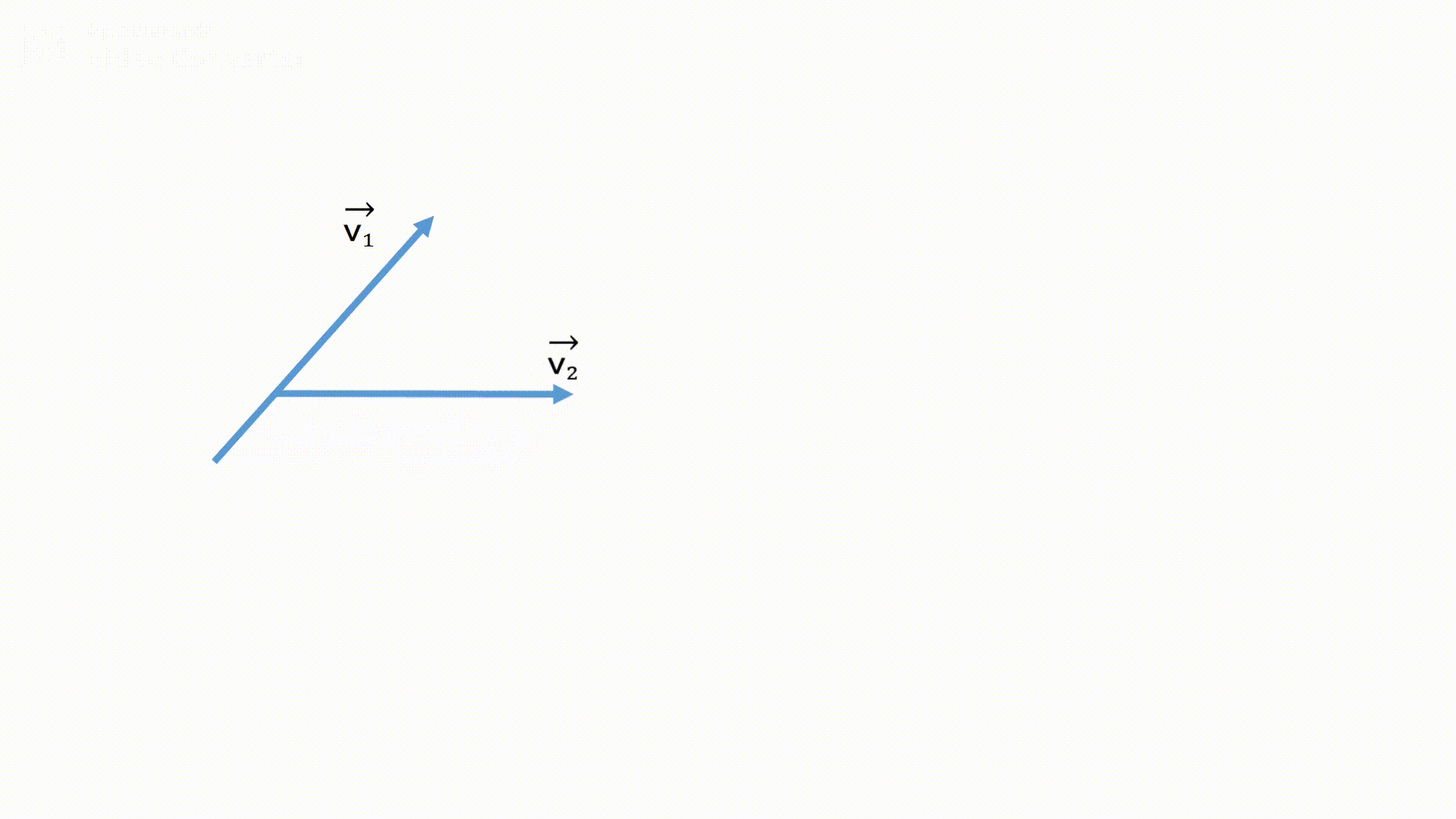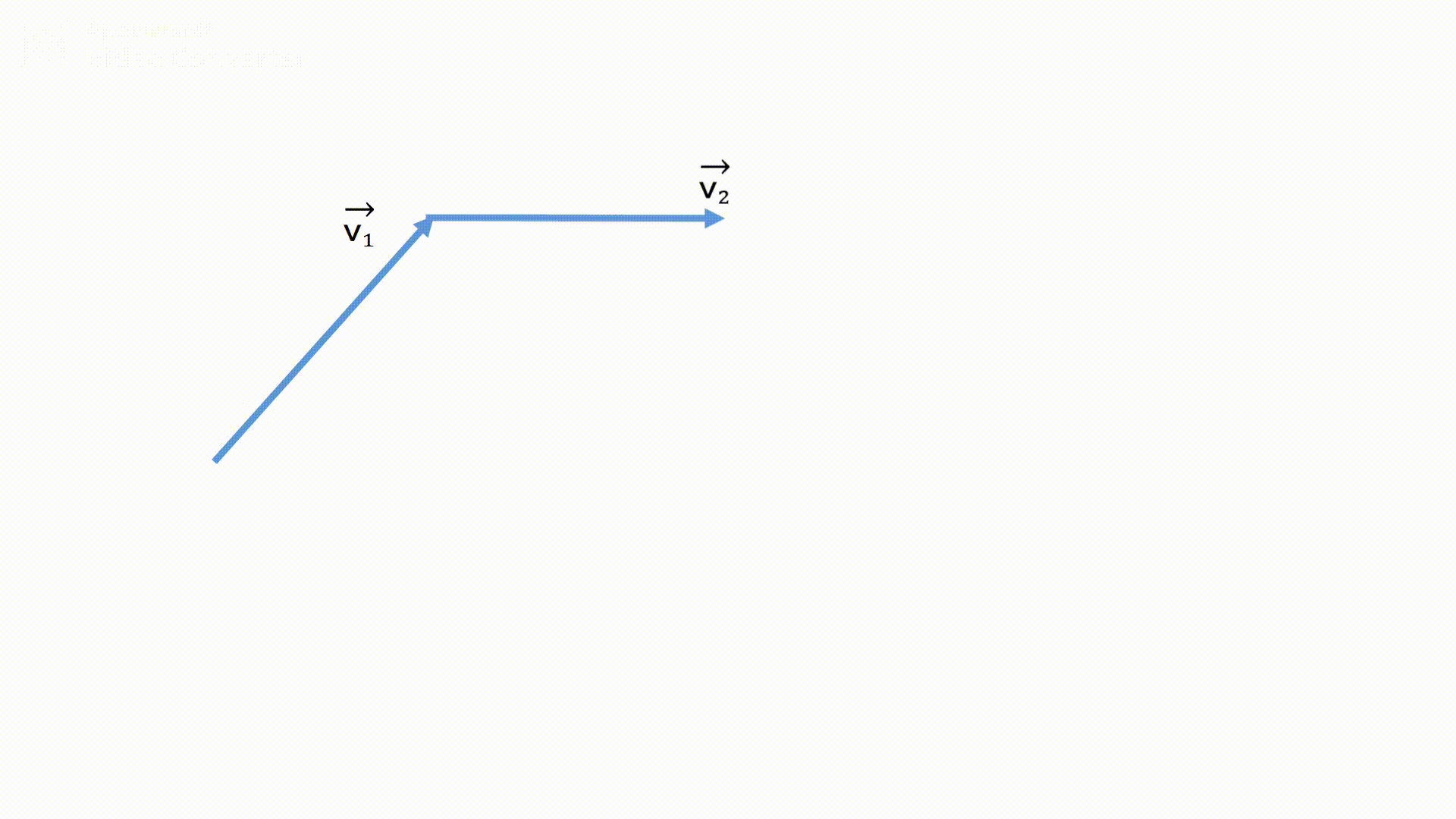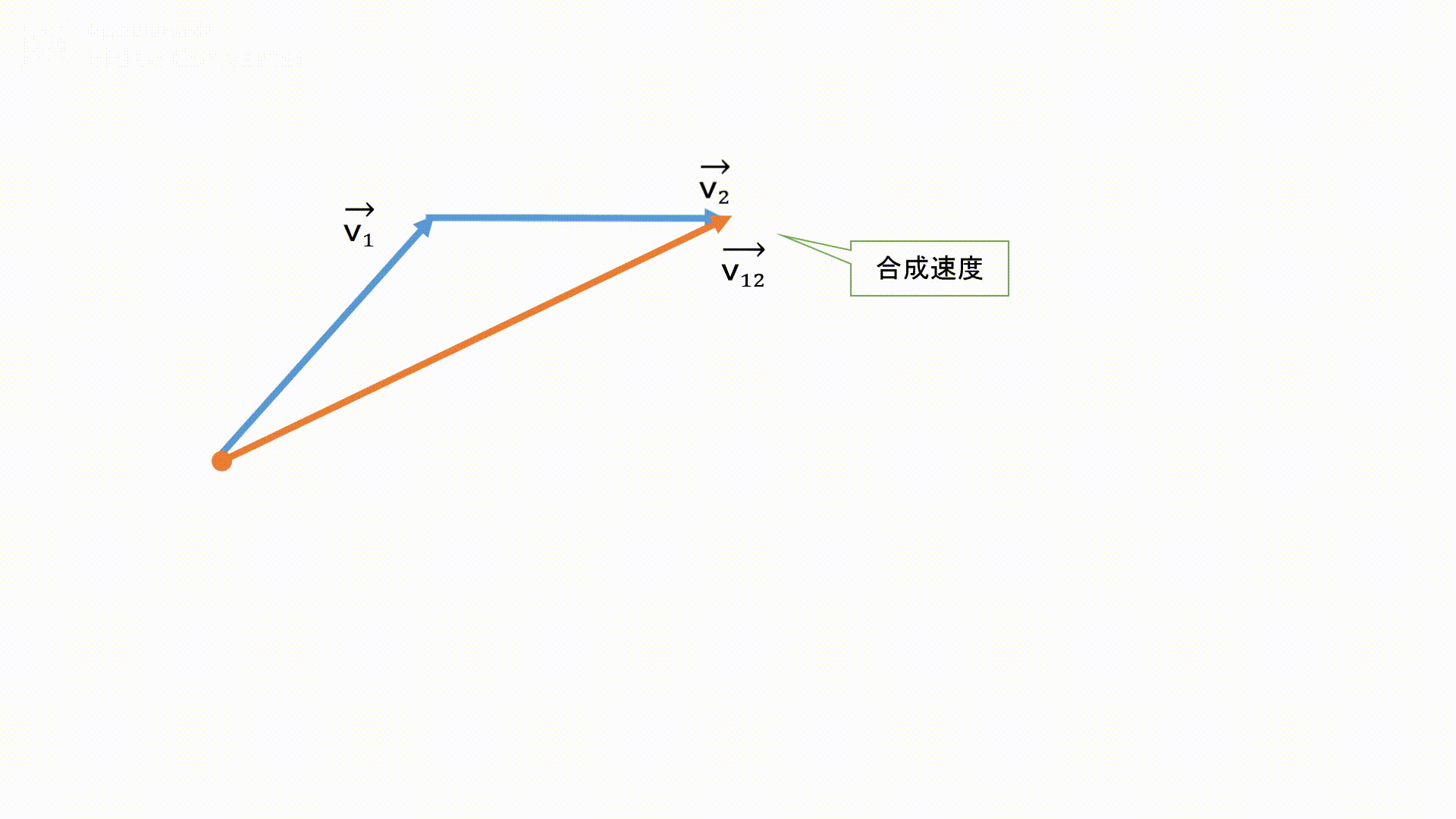
また、矢印の長さを求めるために、三角比か三平方の定理を使用する事が多いです。
相対速度
相対速度とは、2つの物体A,Bが移動しているとき,Aから見たBの速度を指します。
問題文では、Aに対するBの相対速度と表記される事が多く、物理基礎や物理では、~に対する=~から見たと訳して考えていきましょう。
vAB=vB-vA ← vAB は、Aから見たBはを意味します。
一直線上の相対速度
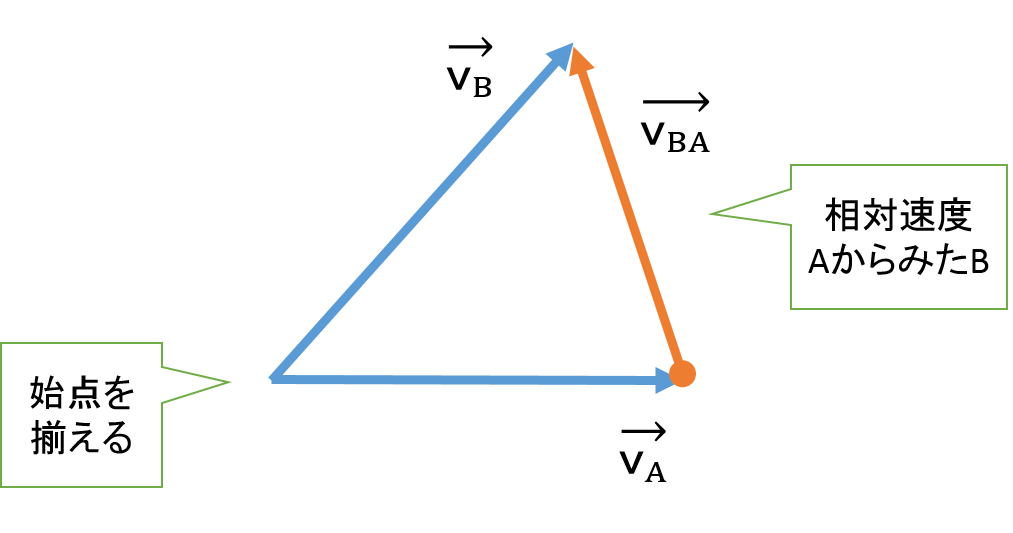
相対速度を図示する際は、以下の手順で行います。
- 二つの速度の矢印の始点を揃えます。
- 見ている対象の矢印の先端から線を引きます。
AからBを見ている場合は、Aの矢印の先端からBの矢印の先端に向かって線を引くと矢印の大きさと向きを出すことができます。
平面上の相対速度
基本的な作図の仕方は、一直線上の相対速度のときと同じ手順ですが、最後の計算の部分で三角比や三平方の定理を用いて解きます。
作図の手順は以下の通りです。
- 二つの速度の矢印の始点を揃えます。
- 見ている対象の矢印の先端から線を引きます。
- 相対速度の矢印の大きさを三角比や三平方の定理を用いて求めていきます。
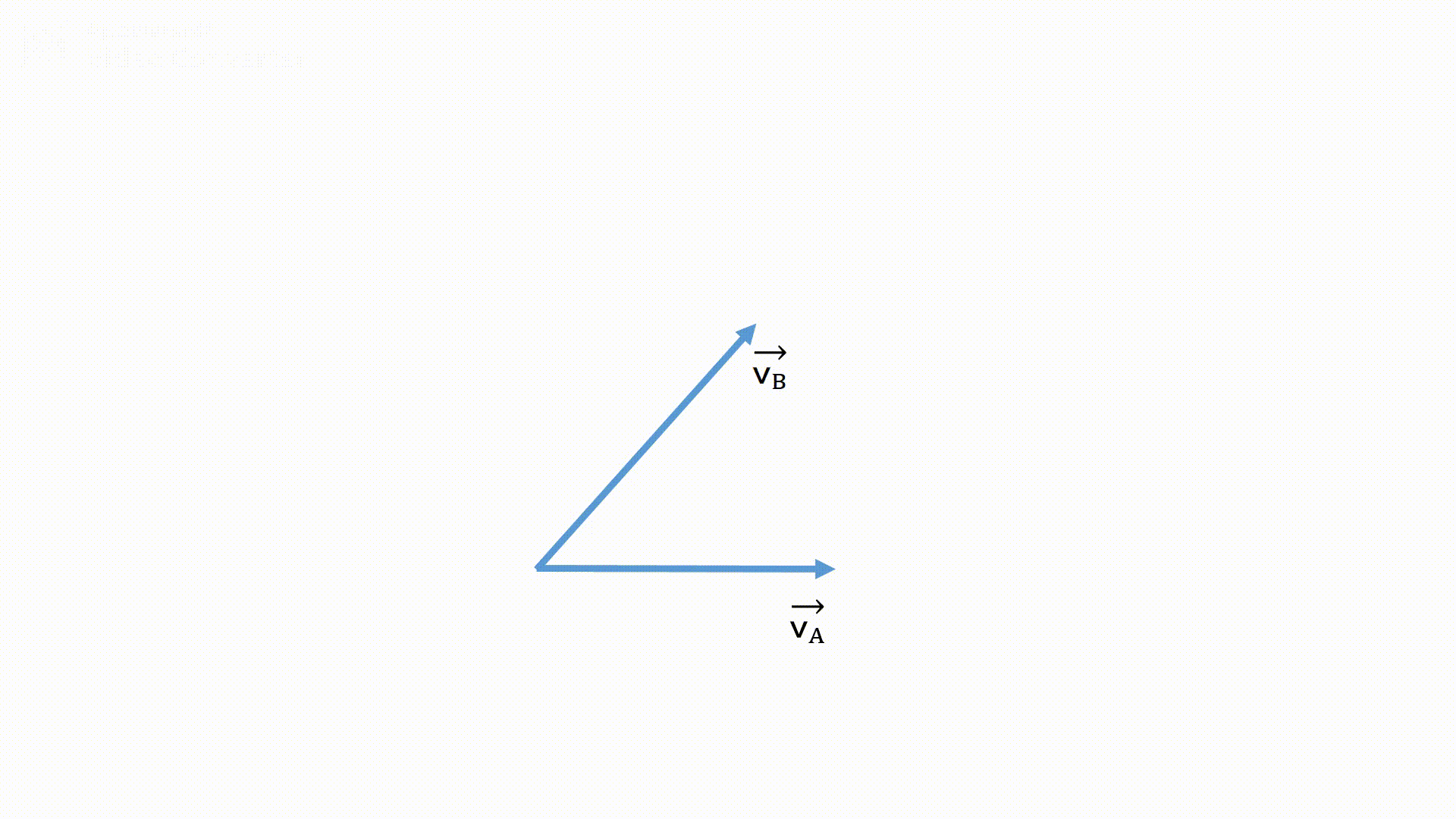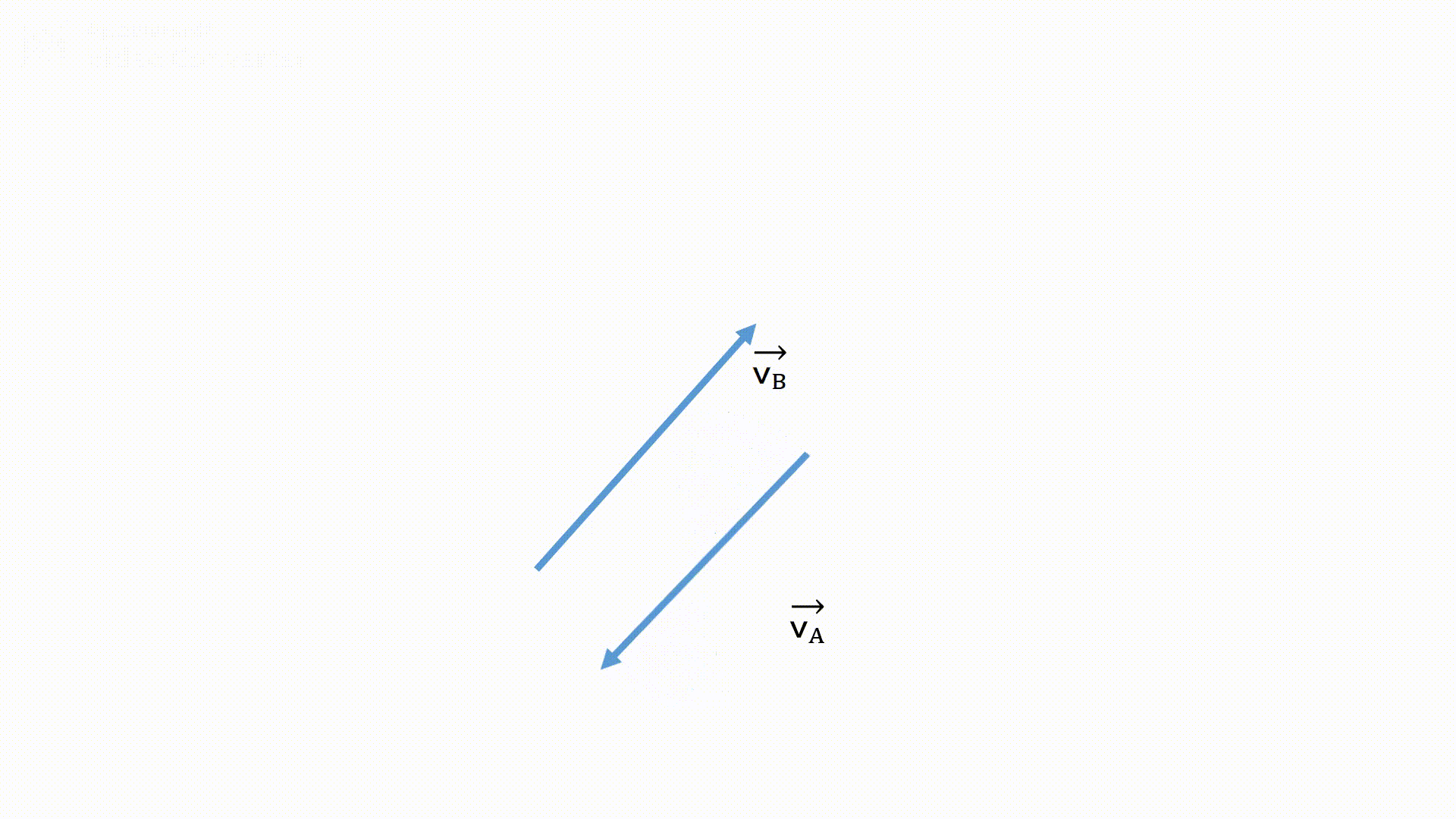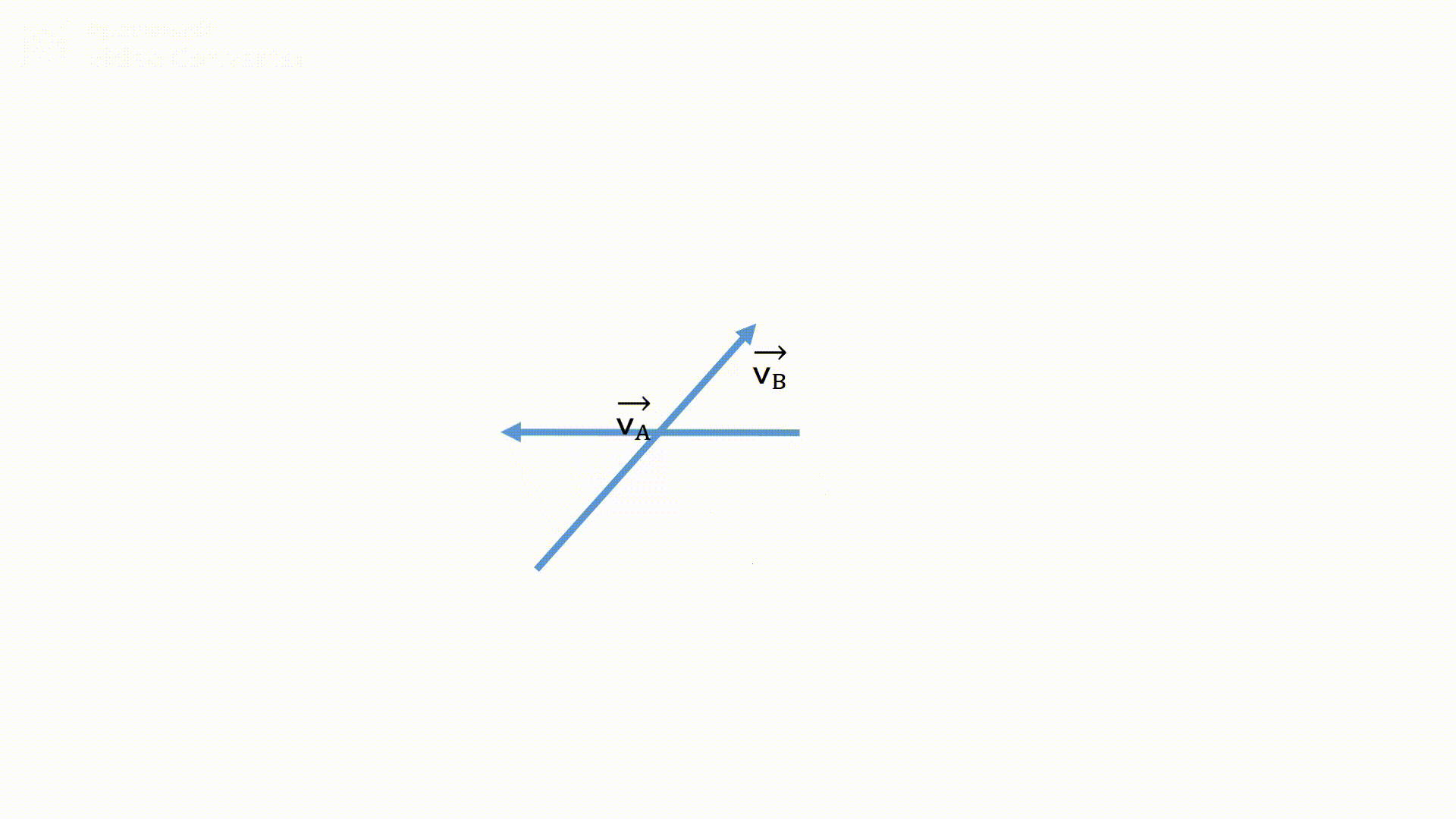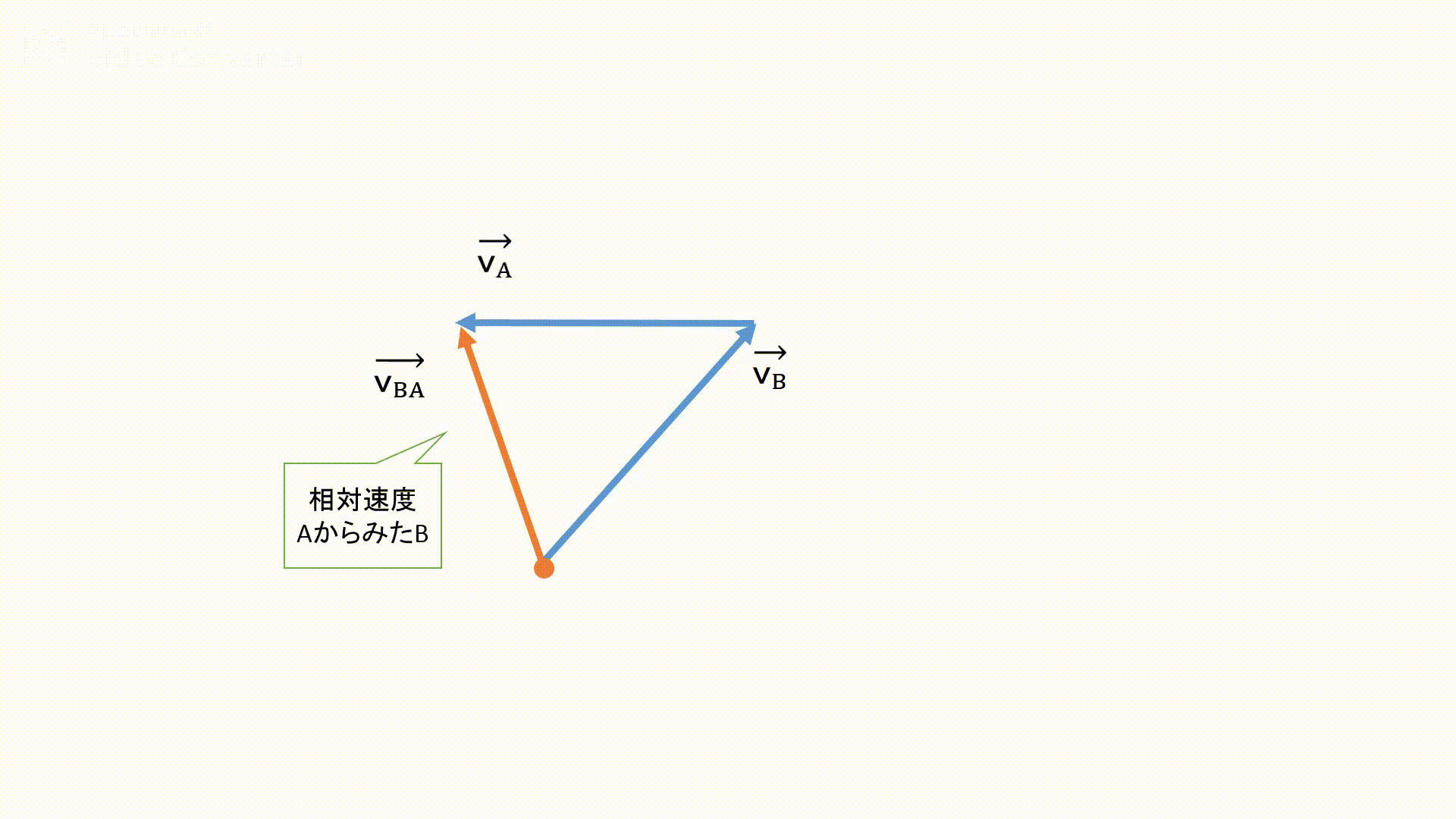
まとめ
合成速度、相対速度の違いや、直線上の場合と平面の考え方が理解できましたか?今回の内容をまとめていきたいと思います。
- 合成速度は、矢印をつないで始点と終点をつないで作図する。
- 相対速度は、矢印の始点を合わせて、見ている対象の矢印の先端から、もう一方の矢印の先端に繋いで作図する。
- 作図した矢印の大きさを求める際は、直線なら値の符号を意識して足し算・引き算を行い、平面なら三角比や三平方の定理を用いる。
二つの速度の作図を間違える人はとても多いと思います。きちんと理解して問題に取り組みましょう。ではでは!ヽ(・∀・)ノ
▽高校教師の私が最もおススメする基礎固めに最適な問題集はコチラ▽
▽センター試験8~9割を狙う受験生におススメする参考書のセットはコチラ▽


コメント