今回は、力の合成と力の分解について学びましょう。
物理基礎や物理を解いていくと、一つの物体に対して力が複数かかってくる事があります。
それらの力を合成したり、分解したりすることによって、問題が解きやすくなることがあります。
力の合成
力の合成とは、物体に複数の力がはたらく際に、それらの力と同じはたらきをする1つの力を求めることです。
求めた力を合力と呼んでいます。
物体は、合力の向きに加速していきます。 ← これかなり重要
2力の合成~平行四辺形の法則~
物体に力が二つはたらく場合、この二つの力を辺と考えて、平行四辺形を作成します。
作図する際は、平行な点線を矢印の先から二つ描き、交わる部分と矢印の始点を繋げる矢印を記入すれば完成となります
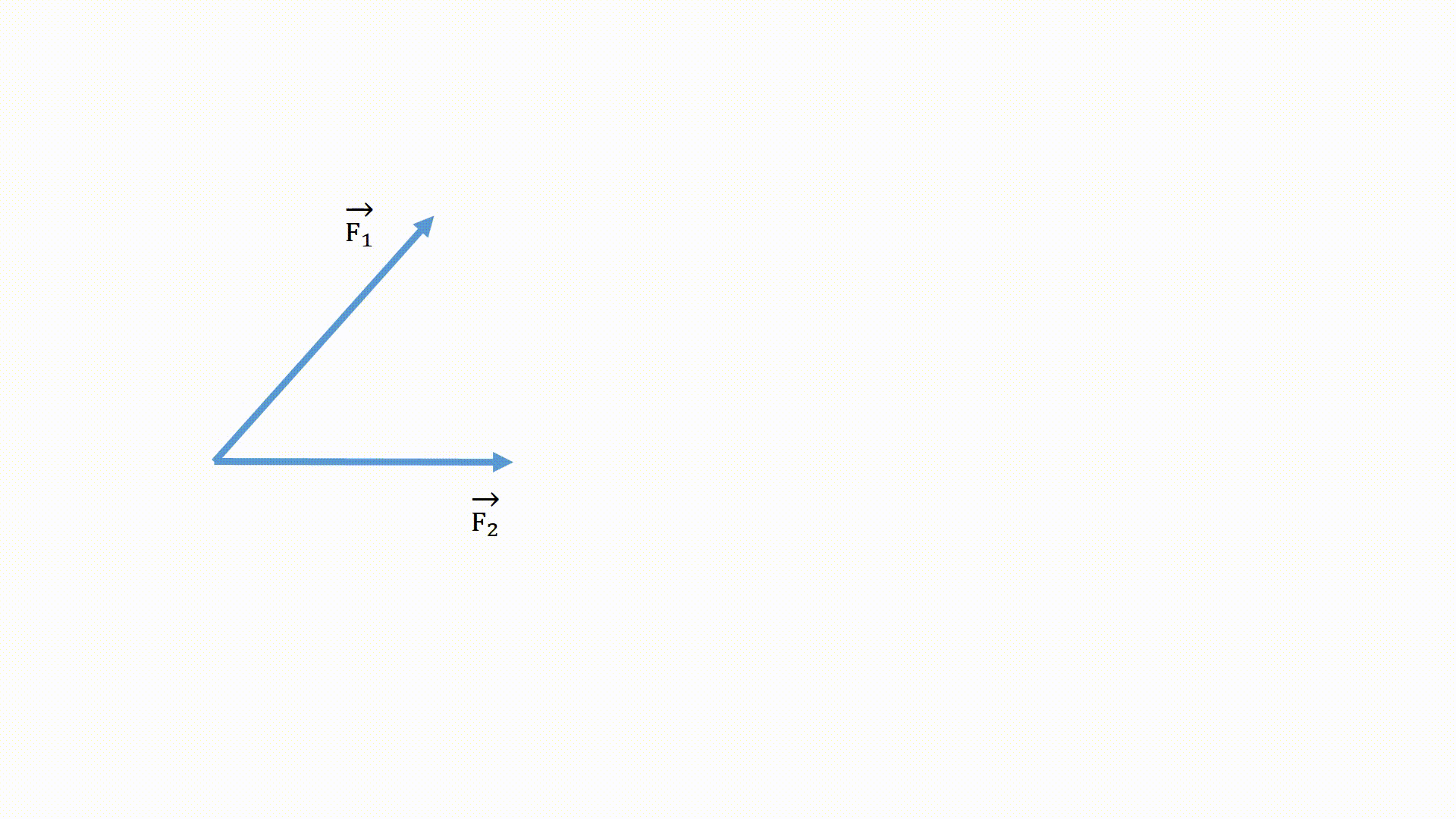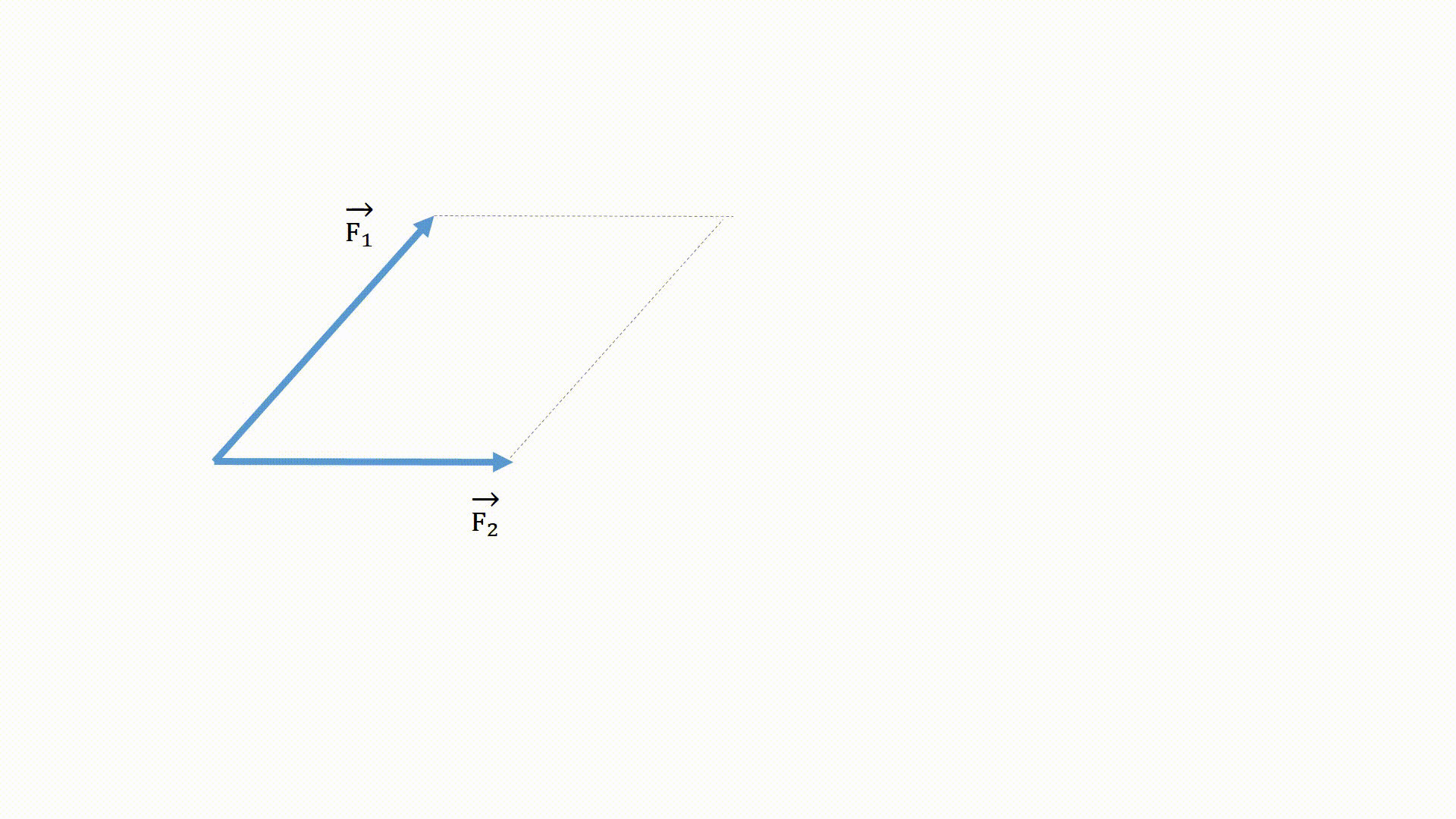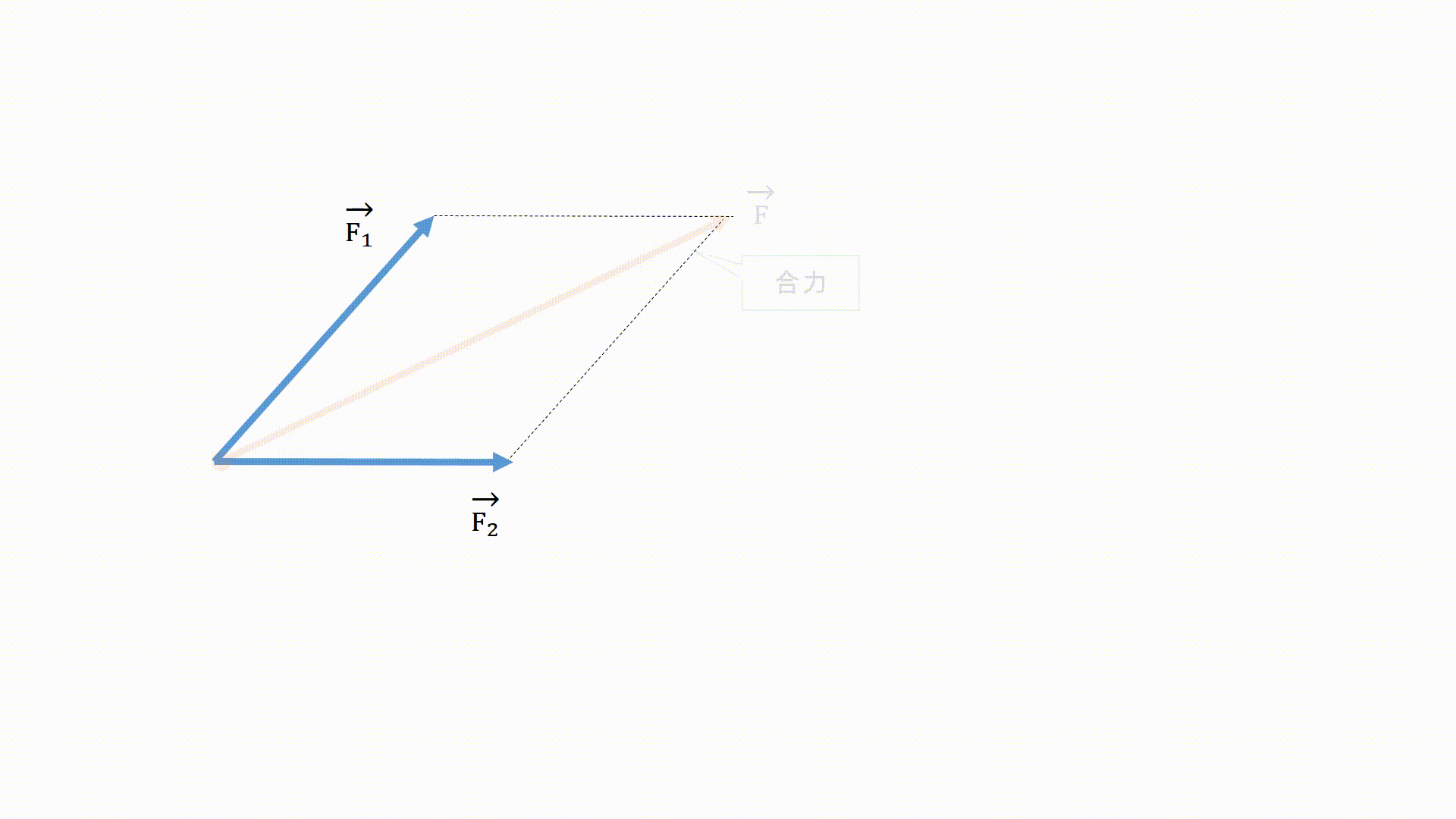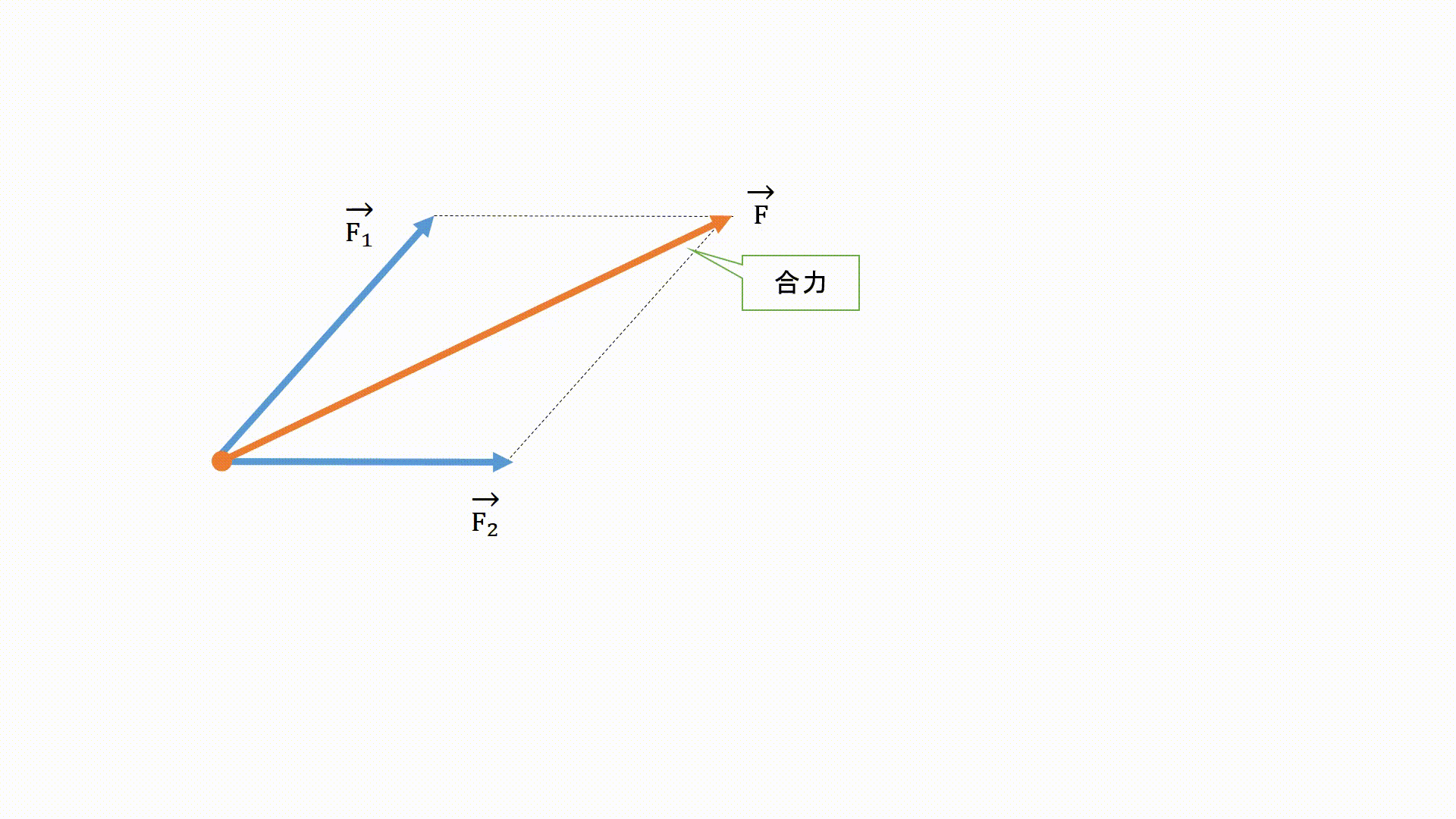
3力の合成 ~複数の力は1つずつ攻略~
物体に複数の力が働く場合は、まず二つの力を合成し、その合成した力と残っている力を合成していきます。

力の分解
力の分解とは、1つの力をそれと同じはたらきをする2つの力に分けることです。
この分けられた力を分力といいます。
基本的に面に平行な成分と、それに対して垂直な成分などに分解します。
これは、計算するときに座標が直角の方が計算しやすいためです。

力の成分
力の成分とは、x軸とy軸をとった際のx方向とy方向の力の大きさのことを指します。
力のx成分をFx、力のy成分をFyと表記します。
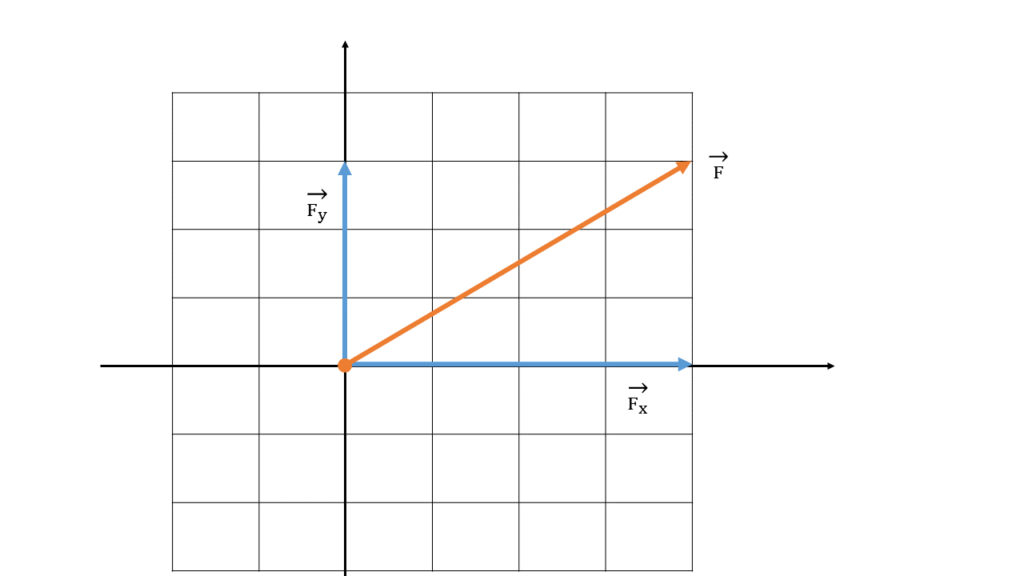
力の成分を求める方法
力の成分を求める際には、マス目があるのか、ないのかがとても重要です。
マス目がある場合
それぞれの軸に沿ってマス目を数えるだけで答えることができます。
この際には問題文に1マスあたり1Nなどの記載がありますので、マス目×1マスあたりの力の大きさで計算を行っていきましょう。
図の場合、1マスを1Nとすると、Fx=4N、Fy=3Nとなります。
マス目がない場合
三角比や三平方の定理を用いて成分を出していきます。

三角比を用いる場合、sinθとcosθの付け間違いがとても多いです。
以下のように覚えましょう。
- 斜辺となす角θを持つ辺 → 斜辺 × cosθ
- 斜辺となす角θを持たない辺 → 斜辺 × sinθ
成分には正と負がありますので、座標軸の矢印の向きをきちんと確認して、符号を付けていきましょう。
まとめ
力の合成、分解を行うことで力をスッキリと図示することができるようになります。では、今回の内容をまとめます。
- 力の合成は、平行四辺形を必ず作る。
- 力の分解は、x軸、y軸に沿って分解する。
- 力の成分は、目盛がある場合は目盛の値をよみ、目盛がないときは三角比や三平方の定理を用いて答えていく。
三角比が苦手な人は、30°、45°、60°が頻出なので、値を覚えておきましょう!
力がはっきりしてくることによって、力のつりあいや運動方程式などの問題が解けるようになりますので、きちんと力の合成、分解できるようになりましょう!ヽ(・∀・)ノ
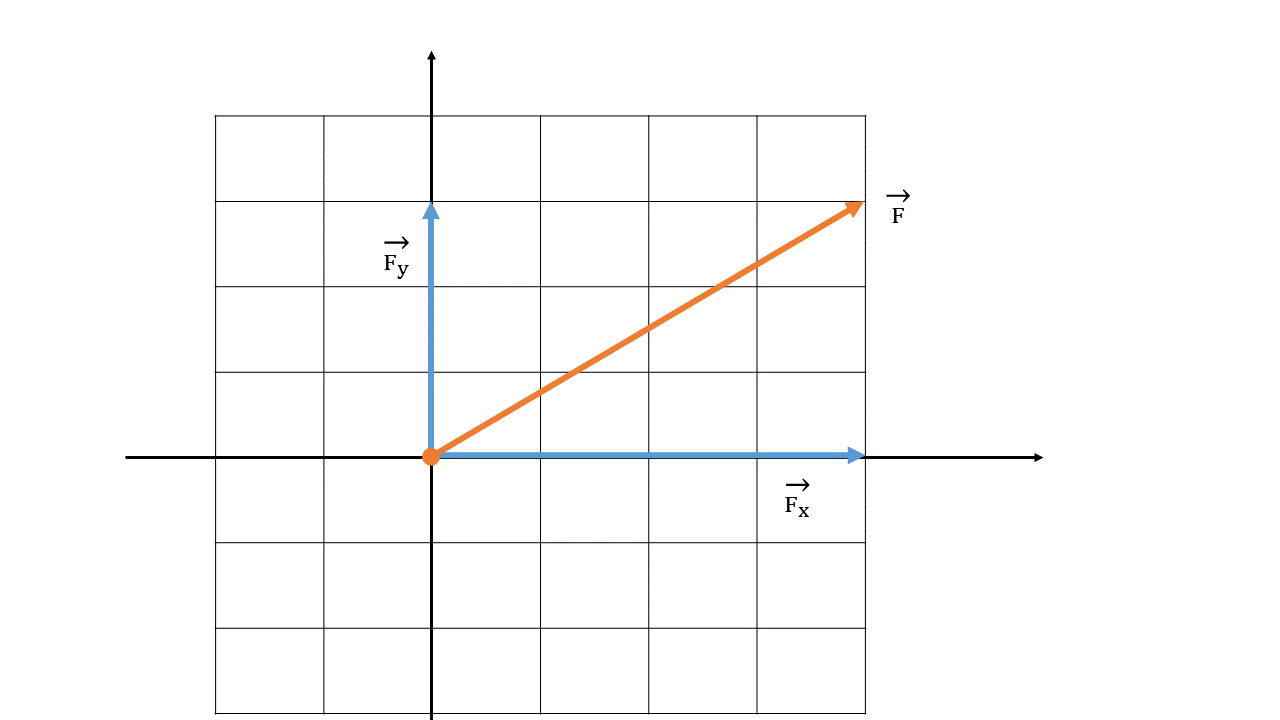

コメント