こんにちは!今回は重力による位置エネルギーについて説明していきたいと思います。
物理基礎の力学分野で出てくる位置エネルギーは主に二つあります。
1つが『重力による位置エネルギー』これから説明するものです。
1つが『ばねによる位置エネルギー』こちらは別でページを用意します。
力学的エネルギー保存の法則を使いこなすためにはどちらの知識も必要不可欠です。
ぜひ両方とも覚えるようにしましょう。
重力による位置エネルギーの公式
まずは、公式の確認です。重力による位置エネルギーは以下の公式で表されます。
U=mgh(重力の位置エネルギー=質量×重力加速度×高さ)
この公式は確実に暗記しましょう。
どのように求めるかも解説していきます。
重力による位置エネルギーの公式を導出する
公式の導出のためには、運動エネルギーの差は仕事という考えを基に解いていきます。
運動エネルギーについて知りたい人は『運動エネルギーの求め方や仕事との関係を理解しよう』という記事を確認しておきましょう。
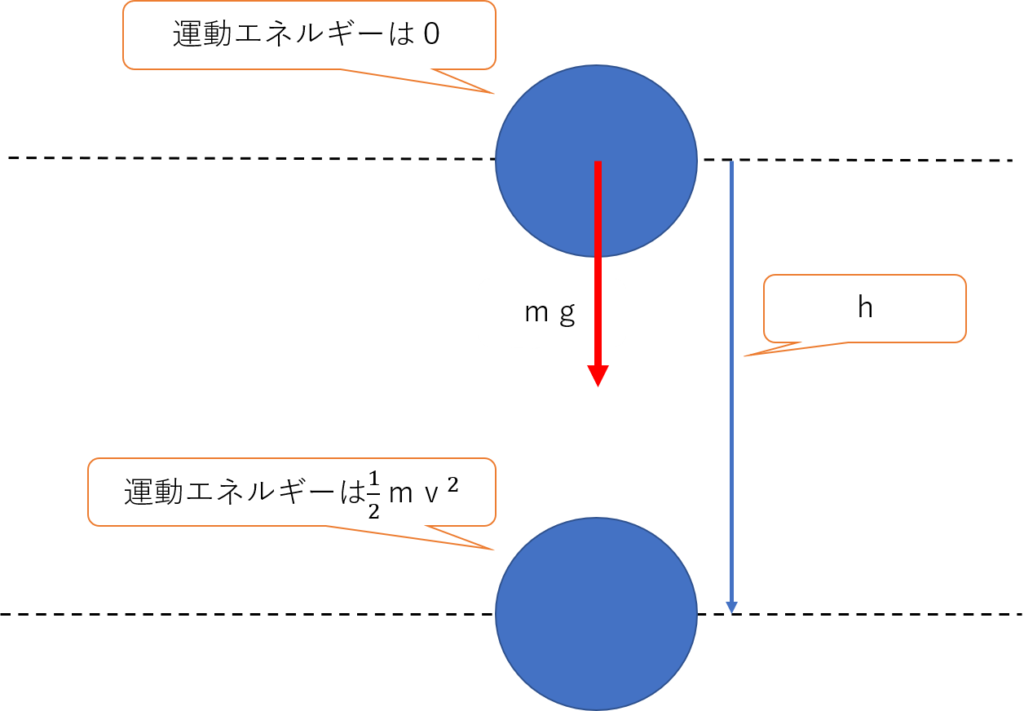
高さを失う代わりに速さが増していきます。
この時に重力がした仕事がW=mg・hなので、
運動エネルギーの変化量は物体がされた仕事と等しいということから、
運動エネルギーはmghということになります。
これは上の位置から下の位置に移動したときに、運動エネルギーが増加したので、その分だけ物体は仕事ができるようになった。
つまり重力がある場合、高さがあるだけでエネルギーを持っているということを表します。
以上の事から、hの高さにある物体は、mghの位置エネルギーを持つということが言えます。
最も重要なのは基準面を把握すること
今回、もっとも重要なのは、基準面をきちんと理解することです。
以下の項目を覚えましょう!
- 重力による位置エネルギーの基準水平面は,自分で決めることができる。(問題文に指定がある場合はそちらを優先)
- 基準面と高さが同じ ・・・ U=0
- 基準面より高さが上 ・・・ U>0 ( Uは正)
- 基準面より高さが下 ・・・ U<0 ( Uは負)
質量mと重力加速度gの値は変化しないので、高さhに関して正負をつけて計算します。
基準面を入れ替えた3パターンの画像を用意しました。
基準面が真ん中の場合

上にある物体は正、下にある物体は負となります。
基準面が一番下の場合

基準面より物体が上にあるので、全て正となります。
全て正なので計算が一番楽だと思います。最もおススメの基準面の位置
基準面が一番上の場合
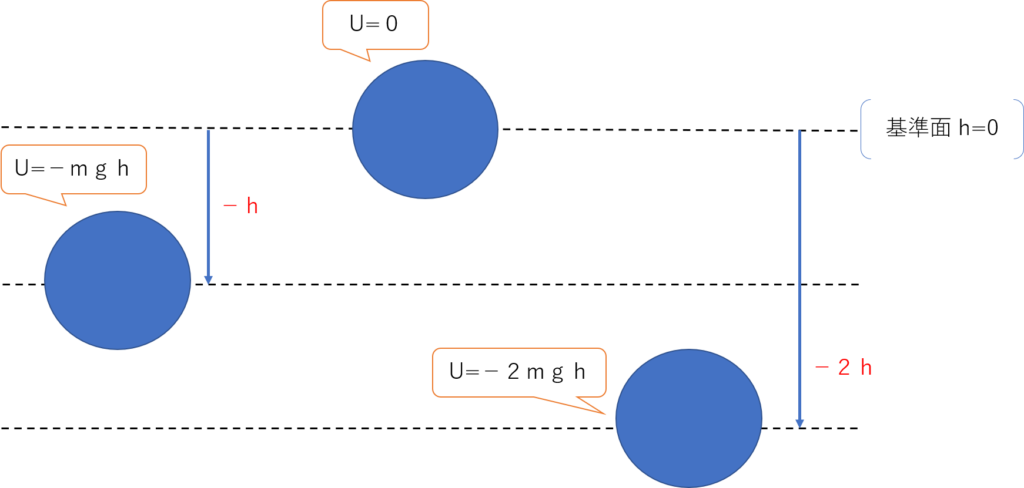
基準面より物体が下にあるので、全て負となります。
まとめ
重力の位置エネルギーのイメージはつかめたでしょうか?
以下の内容を抑えましょう。
- U=mghは大きさを出すためにある公式。
- 基準面からの位置で正負の符号を決定する。
- 基準面の位置は自分で決めてもよい。(問題文に指定がある場合はそちらを優先)
ちなみに2つ物体があるときは、それぞれで基準面を決めても構いません。
また、(1)(2)など設問ごとに基準面を変えても構いません。
結構自由度が高いので、自分なりにやりやすい方法を模索するのも面白いかもしれません。
頑張って解きましょう!ではでは~!(*‘∀‘)


コメント