こんにちは!今回は3力のつりあいについて学びましょう!
3力のつりあいで力の大きさを求めるには、
- 力の成分で解く方法
- 三角形を作って辺の長さを求めて解く方法
の二つがあります。
問題によって使い分けるのが一番良いですが、解く際のメリット・デメリットも記載していきますので、きちんと読んで自分に合っている方法を使うことをオススメします!
3力のつりあいの定義

物体にはたらく3つの力がつりあうとき,これらの合力は0となる。
これが3力のつりあいの定義となります。(複数の力がはたらく場合もこの条件を満たせばよい。)
このとき,合力の成分も0となるので,x成分y成分の合力もそれぞれ0にならないと定義が成り立ちません。

それでは、2種類の考え方を紹介していきます。
力の成分で解く方法
力の成分で解く場合は、力の分解が必須事項になります。力の分解が苦手な人は、力の合成・分解のページを先に読みましょう♪
上の図をもとにして式を立ててみるとこのようになります。

力を分解し、座標ごとに式を立てて、連立方程式として解いていく方法です。
メリット
- 力が複数以上でも使用可能
- 計算ミスが少なくなる。
3力の力のつりあい<力の成分で解く場合の手順>
- 物体にはたらいている力を全て図に書き込む。
- x軸,y軸にたいして軸に沿っていない力があればその力を分解する。
- x軸,y軸の力のつりあいの式を立てる。
- 連立方程式を解き、答えを求める。
実際に問題を解いてみましょう。
軽い糸1に重さ3.0 Nの小球をつけ,天井からつるす。小球を糸2で水平方向に引き,糸1が天井と60°の角をなす状態で静止させた。糸1が小球を引く力の大きさT1〔N〕と糸2が小球を引く力の大きさT2〔N〕と求めよ。

各成分の力のつりあいの関係より,
x成分 T1cos60°=T2 ・・・①
y成分 T1sin60°=W ・・・②
sin60°、cos60°、W=3.0N を代入し、連立方程式として解いていくと、
T1=2.0×1.73=3.46≒3.5N
T2=1.73≒1.7N
を求めることができます。
矢印で三角形を作って辺の長さを求める解き方

ベクトルの値が0は、矢印を全て繋げることができるという意味をもつため、3つの矢印を繋げて三角形を作り、矢印の長さを求めていく方法です。
メリット
直角三角形であれば、三角比や三平方の定理を用いて、すぐに解くことができる。
3力の力のつりあい<三角形を作って辺の長さを求める解き方の手順>
- 物体にはたらいている力を全て図に書き込む。
- 3本の矢印で三角形を作る。
- 三角比か三平方の定理を用いて矢印の長さを求めていく。
例題(上の問題と同じ問題です)
軽い糸1に重さ3.0 Nの小球をつけ,天井からつるす。小球を糸2で水平方向に引き,糸1が天井と60°の角をなす状態で静止させた。糸1が小球を引く力の大きさT1〔N〕と糸2が小球を引く力の大きさT2〔N〕と求めよ。


まとめ
3力のつりあいは解けるようになりましたでしょうか?
両方に共通しているのは、図に力を描くという作業です。
正しく力を図示できない人は、力の描き方をまず覚えましょう。
では、今回のまとめを行っていきたいと思います。
- 図に力を描けることがスタートライン
- 複数の力がある場合は、力の成分を使って解く方法が確実
- 三角形の辺の長さを用いて解けるのは直角三角形か正三角形の時ぐらい(正弦定理や余弦定理を使えば解けますが手間がかかります…)
物理基礎で2番目の壁となるのは3力のつりあいだと思います。
ここさえ理解できれば、あとは力の種類(公式あり)が増えていくのみです!
まだ増えるんかい...|゚Д゚)))は無しで!(笑)
頑張っていきましょう!ヽ(´▽`)/
▽高校教師の私が最もおススメする基礎固めに最適な問題集はコチラ▽
▽センター試験8~9割を狙う受験生におススメする参考書のセットはコチラ▽

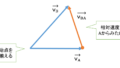

コメント