こんにちは!今回は、a-tグラフ(加速度-時間グラフ)について説明します。
高校の物理基礎や物理の教科書には、x-tグラフやv-tグラフについては、結構丁寧に書いてあるのですが、a-tグラフについての記載はあまり書かれていません。
誠に残念ながら、「教科書に説明なくても意味わかったでしょ?」的なニュアンスなのか、少し難しい問題になると普通に出てきたりします。
物理会は手加減なしですね(笑)
そして、「なんだこのグラフは…?」となる生徒も多いので、説明しておこうと思いました。
説明していきたいと思いますが、その前にx-tグラフとv-tグラフについて自信がない人は復習をする必要があります。
物理基礎③x-tグラフ、v-tグラフを先に読んでおいてください。
a-tグラフ(加速度-時間グラフ)とは
a-tグラフの特徴は、
- 縦軸に加速度a
- 横軸に時間t
を置いていることです。
あと、グラフが出るときには、傾きか面積がなんらかの物理量を示していないかチェックします。
加速度が入りつつ、時間も入っている公式の中で最もシンプルなのが、
v=at(速度=加速度×時間)
の公式です。もう少し細かく書くと、
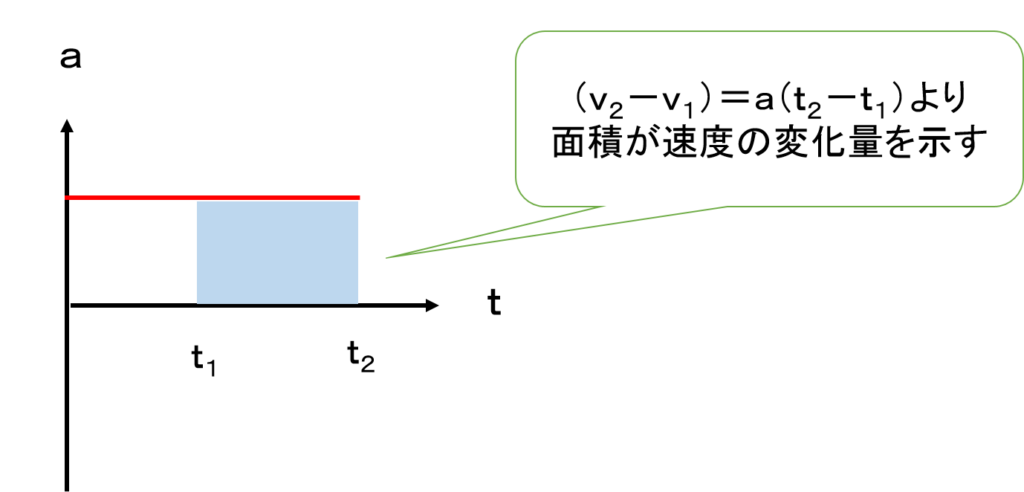
(v2-v1)=a(t2-t1) (速度の変化量=加速度×経過時間)
と表されます。
加速度×時間 は 縦軸×横軸 を示すので、面積が速度の変化量を示します。
a-tグラフをv-tグラフに直す方法
a-tグラフの面積が速度を示すことがわかったと思います。
次のステップとして、v-tグラフに直すことがまず第一目標になります。
まず、行う作業は面積を求めて速度を出していく作業です。
間違いやすいのが等加速度直線運動の場合、時間の区切り方が同じ時間であれば、面積の値が等しくなってしまい、一定速度のグラフを描いてしまうことです。
その時刻の速度を求めたい場合、最初の時刻からの全ての面積を求める必要があります。

正の加速度、加速度0、負の加速度と変化した場合のv-tグラフ
①正の加速度の時は、速度も正の値で増えていきます。
②加速度が0の場合、速度は変化しません。
③加速度が負の場合、面積の値を引いていきます。

v-tグラフからa-tグラフに直す方法
今度は逆にv-tグラフからa-tグラフを書く方法を説明します。
v-tグラフの傾きは加速度を示すので、各区間毎の傾きを求めていきます。
下の図はざっくりとした感じですが、
①正の傾きは、正の加速度
②傾き無しは、加速度が0
③負の傾きは、ふの加速度
を示しています。

また、グラフ全体では、加速度が変化していて等加速度直線運動とは言えません。
傾きが区間で変動していないので、その区間ごとには、等加速度直線運動であることがわかります。
a-tグラフからx-tグラフに直す方法
a-tグラフからx-tグラフにしたい場合、間にv-tグラフを挟みます。
以下の手順で解きます。
- a-tグラフの面積から速度vを求め、それを元にv-tグラフを作成。
- v-tグラフの面積から変位xを求め、それを元にx-tグラフを作成。
a-tグラフ ⇔ v-tグラフ ⇔ x-tグラフ
このように間にv-tグラフを挟めば必ず解けるようになっています。
a-tグラフが出てくるタイミング
加速度が入る公式は多々ありますが、物理基礎の範囲に出てくるものは、等加速度直線運動の問題が多いです。
物理基礎の運動方程式も基本的には、等加速度直線運動です。
たまに速度の変化が等加速度運動ではない空気抵抗を含む終端速度などのv-tグラフが出たりしますが、そのような問題の場合は時間毎に計算することはほぼ出ません。
計算するとしてもv-tグラフのある点の瞬間の加速度を求めるぐらいです。
a-tグラフの形を聞かれるので、v-tグラフの傾きを元に形を推測していきます。
まとめ
a-tグラフについて、ざっくりとお話しました。
グラフの種類が増えて、少し大変と感じていませんか?
最終的な目標は、「グラフを自分の力で作成する」事です。慣れたら誰でもできます♪
とりあえず、今回の内容をまとめておきたいと思います。
- a-tグラフの面積は速度の変化量を示す。
- 該当する自国の速度を知りたい時はt=0からの全ての面積を計算する。
- a-tグラフ⇔x-tグラフの変換にはv-tグラフを挟む。
大学入試のレベルになると、グラフの変換の問題はよく出てくるので、公式を元にグラフのどの部分がどこを指しているか理解しておく必要があります。
なぜ、こんなにもグラフが増えてきたのかですが、実は、大人になって仕事を始めると、様々なデータをグラフ化して、いかに見やすくするかとか、グラフから何を読み取れるかなど、データを元にメリット、デメリットに気づく力を社会で求められます。
物理はまだ、公式が用意されているのでマシなほうだと思います。(笑)
なんだかんだ、何回も解くと慣れてくるので、復習も忘れずに行っていきましょう♪


コメント