こんにちは!今回は運動方程式について学んで行きます!ちなみにこの分野は、求められる能力がとても多いです。力の図示、力の分解、運動方程式を立てる…今までの物理力を試してくるかのような雰囲気があります(笑)頑張って乗り越えましょう!
運動方程式とは!
運動の法則から導かれる公式を指します。

いたってシンプルな式ですが、実は合力Fの組み合わせパターンは無限に増やすことができます!かといって、極限とかしませんけど…(笑)
とにかく、合力Fの部分を正確に代入できる人は確実に解けます!
合力を書く手順を思い出そう!
下の方に運動方程式の解く手順を紹介していきますが、そもそも力を図示できない人は解けません。ということで、力の図示の仕方を復習しましょう!
力の図示の仕方
- 重力を図示する。
- 触れているものからはたらく力を図示する。(垂直抗力、張力、摩擦力、弾性力など)
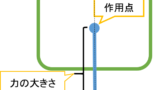
図示するときに大事なのは、作用点と力の向きをきちんと把握しているかということです。忘れた人は、一旦戻りましょう!
運動方程式の使い方
- 運動方程式を立てる物体を決める。
- 物体が受けている力をすべて図示する。
- 正の向きを定め、a(加速度)と記入する。基本、物体が運動する向きを正とする。
- 物体が運動する向きの力の成分の和(合力)を求める。(上下に動くならy成分、左右に動くならx成分)
- 力の成分の和を,運動方程式ma=Fに代入する。
実際に運動方程式を立ててみよう。
水平面上に質量1.0kgの物体が置かれている。この物体に右向き10N、左向きに5Nの力を加えた。この物体の加速度はいくか答えよ。
①~⑤の手順を見てみてください。
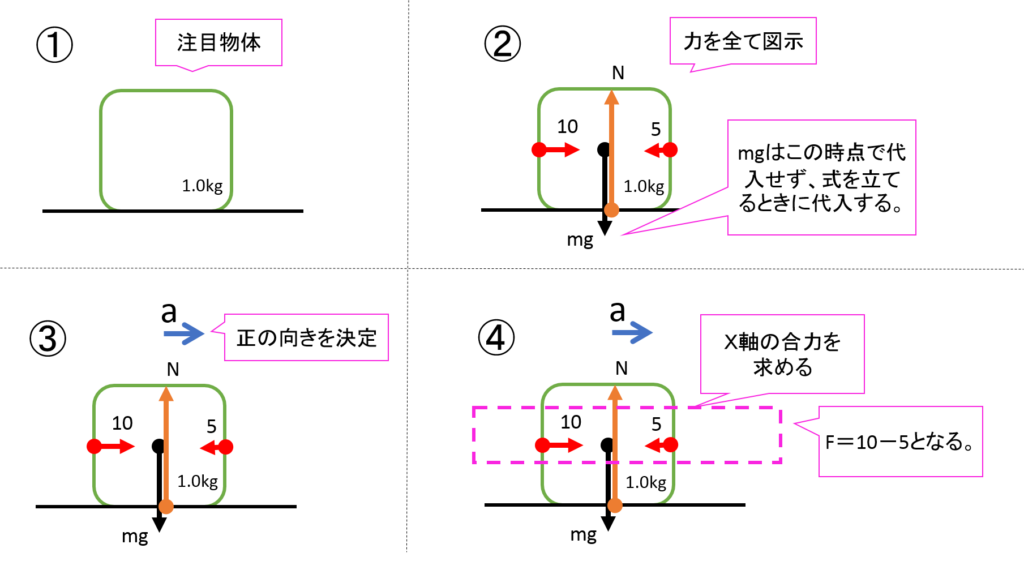

⑤運動方程式に代入する。
1.0×a=10-5 a=5
式まで立てることができればあとは物理量を求めるのみなので、計算自体は難しくないことが多いです。
運動方程式 斜面の問題の解き方
斜面の問題を解くことができれば、1物体の運動方程式の問題はほぼ解けると思います。
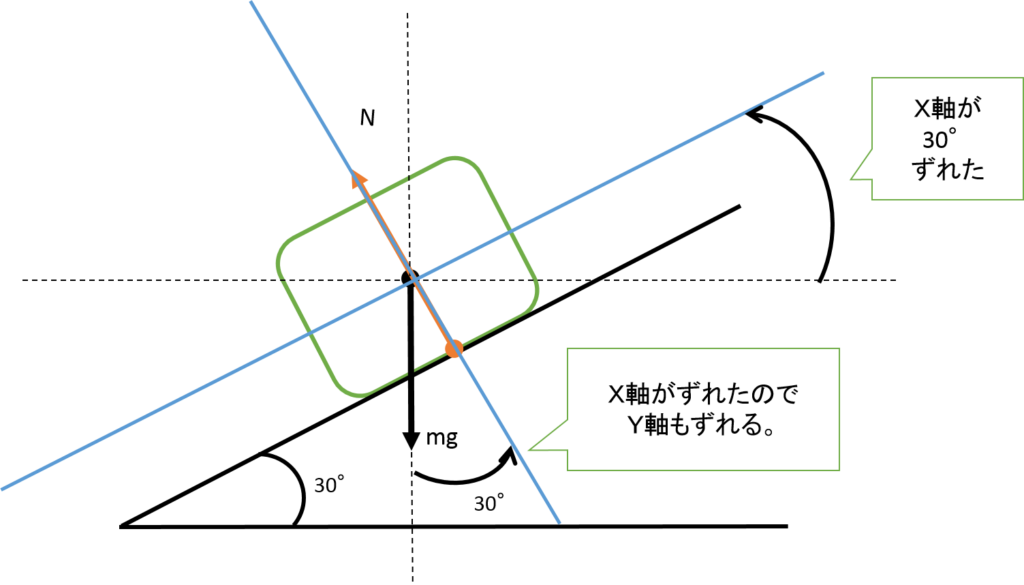
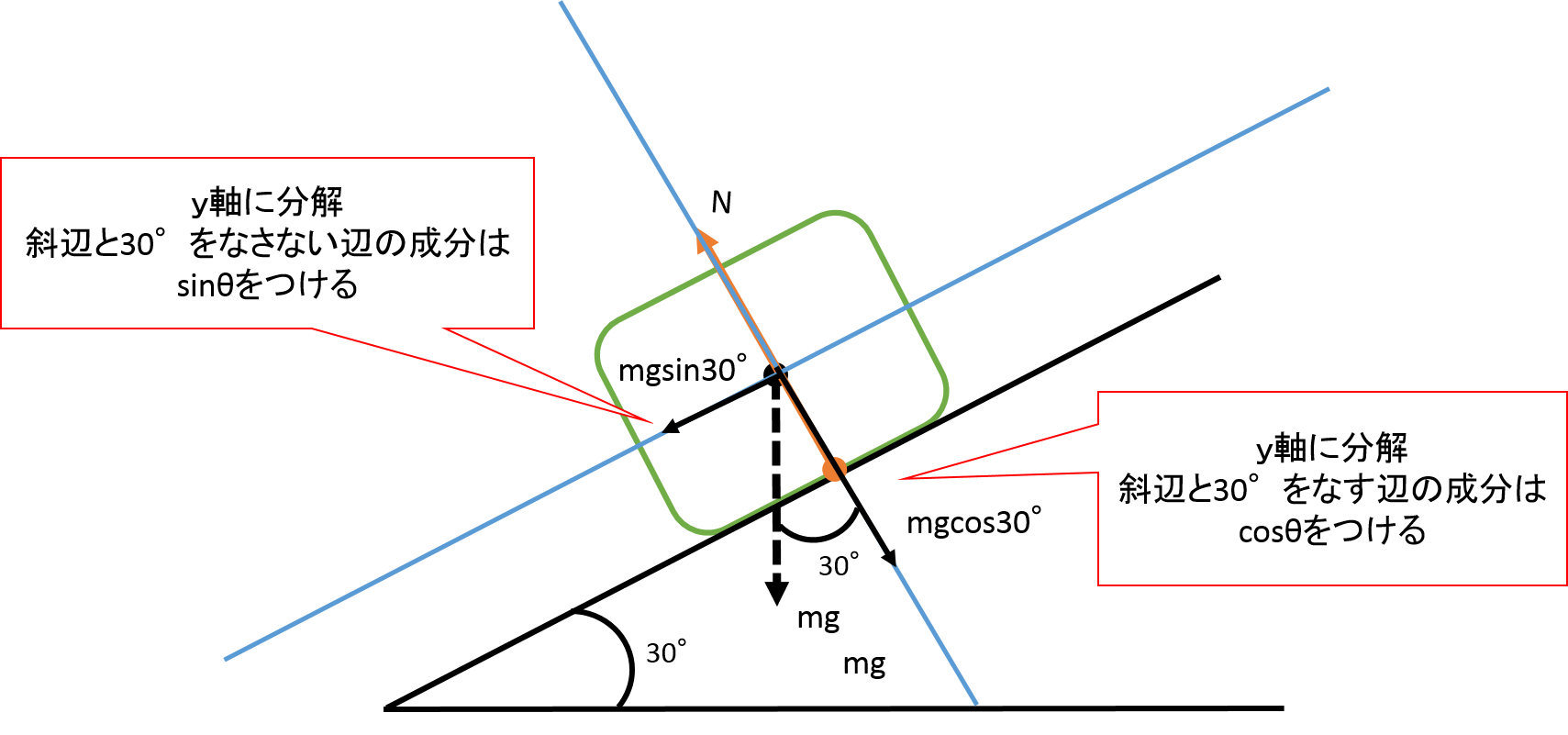
大切なのは、どの成分を使うのかきちんと把握できるように図示することです。軸の決め方で最も多いミスは、角度のつける部分を間違えることです。角度を間違えると成分の値が変わります。 きちんと書けるように下の図を見てみましょう。
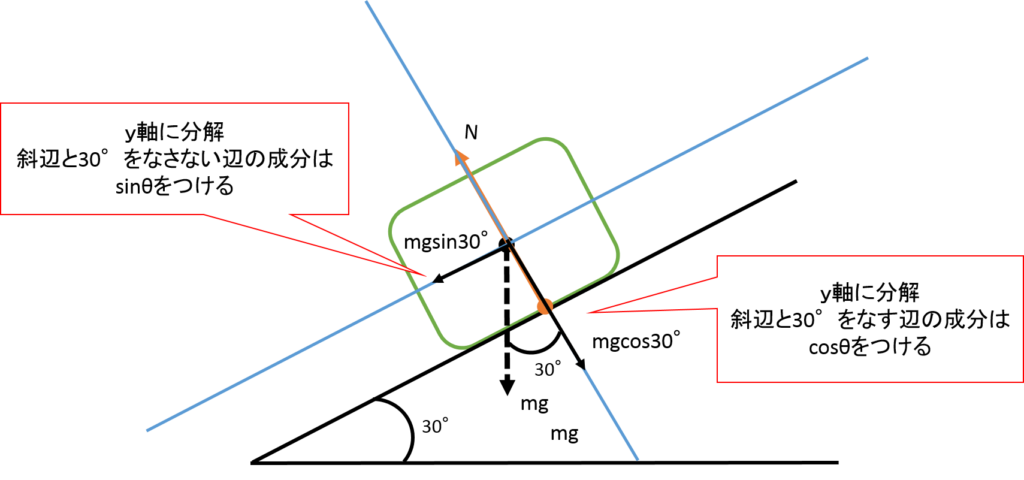
斜面の力の分解

斜面になると重力を分解する必要が出てくることがわかります。ここで大切なのはsinθとcosθをつけ間違えないようにすることです。

運動方程式の解き方に当てはめてみましょう。
図は、重力を受けて滑り降りていく物体を表しています。
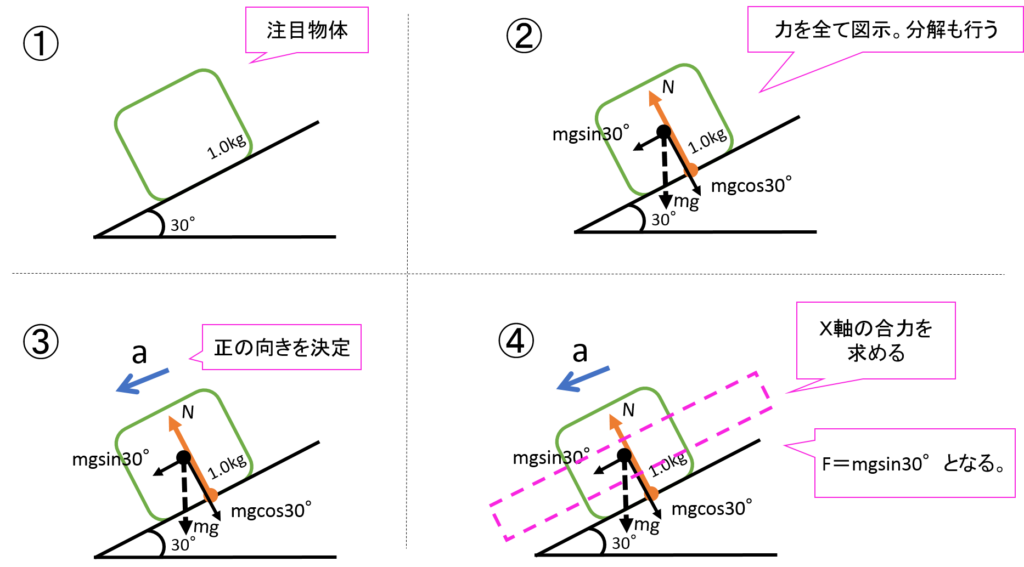

⑤運動方程式はma=mgsin30°となります。
あとはm=1.0、g=9.8、sin30°の値を代入すれば問題を解くことができます。
まとめ
運動方程式の立て方は分かりましたか?きちんと図示して、運動の向きをきめて、落ち着いて解くことができれば問題なく解くことができると思います。では、まとめていきましょう。
- 図に力をきちんと描かないと合力Fが代入できない。
- 加速度の向き(正の向き)のみの力の成分しか使わない。
- 式を立てれば計算はとても簡単。
運動方程式は問題のバリエーションがとても多いです。簡単な問題集で演習を行い、基礎力を身につけましょう!では!ヽ(´▽`)/


コメント